4 Exemplos De Soma De Vetores No Mesmo Sentidos Opostas? Incrível, né? Tipo, vetores são, sabe, essas flechinhas que mostram força e direção. A gente vai mergulhar fundo nessa vibe de somar essas flechinhas, tanto quando elas apontam pro mesmo lugar, quanto quando estão em lados opostos. Prepare-se para um rolê matemático maneiro, cheio de exemplos práticos pra você não ficar boiando.
Vai ser tipo, super fácil de entender, juro!
A soma vetorial é chave pra entender um monte de coisas, desde o movimento de um carrinho de rolimã até as forças que agem num objeto. A gente vai ver como somar vetores que seguem na mesma direção e sentido, e depois o que acontece quando eles estão em sentidos opostos. Usaremos gráficos e cálculos, tudo bem explicadinho, pra você não se perder.
E no final, alguns exemplos do mundo real pra você usar esse conhecimento na prática e mandar ver!
Soma de Vetores: Mesmos Sentidos e Sentidos Opostos: 4 Exemplos De Soma De Vetores No Mesmo Sentidos Opostas
Vamos explorar o mundo da soma de vetores, um conceito fundamental na física e na matemática. Veremos como somar vetores que apontam na mesma direção e no sentido contrário, aprendendo a calcular o vetor resultante e a visualizar graficamente esses processos. A compreensão desses conceitos é crucial para resolver problemas em diversas áreas, desde a mecânica clássica até a programação de jogos.
Introdução à Soma de Vetores
Um vetor é uma grandeza física que possui tanto magnitude (tamanho) quanto direção e sentido. Graficamente, representamos um vetor como uma seta, onde o comprimento da seta representa a magnitude e a orientação da seta indica a direção e o sentido. A direção é dada pela linha de ação do vetor, enquanto o sentido é indicado pela ponta da seta.
Na soma vetorial, a direção e o sentido são absolutamente cruciais, pois a soma não é simplesmente uma adição aritmética dos módulos. Vetores com o mesmo sentido apontam na mesma direção, enquanto vetores com sentidos opostos apontam em direções opostas ao longo da mesma linha de ação.
Soma de Vetores com o Mesmo Sentido

Quando somamos vetores com o mesmo sentido, o vetor resultante tem a mesma direção e sentido dos vetores originais. Sua magnitude é simplesmente a soma das magnitudes dos vetores componentes. O método é intuitivo: basta somar os módulos. A magnitude do vetor resultante será sempre maior do que a magnitude de qualquer um dos vetores individuais.
| Exemplo | Vetor 1 | Vetor 2 | Vetor Resultante |
|---|---|---|---|
| Deslocamento | 5m para leste | 3m para leste | 8m para leste |
| Velocidade | 10m/s para norte | 5m/s para norte | 15m/s para norte |
Observe que a representação gráfica seria duas setas na mesma direção e sentido, com o vetor resultante sendo uma seta maior, com o mesmo sentido e direção, e com comprimento igual à soma dos comprimentos das setas originais.
Soma de Vetores com Sentidos Opostos
Quando os vetores têm sentidos opostos, o vetor resultante terá a direção dos vetores originais, mas o sentido será o do vetor com maior magnitude. Para calcular o vetor resultante, subtraímos o módulo do vetor menor do módulo do vetor maior. A representação gráfica mostra duas setas na mesma linha, mas apontando em direções opostas. O vetor resultante terá o sentido do vetor maior e um comprimento correspondente à diferença entre os módulos dos vetores originais.
| Exemplo | Vetor 1 | Vetor 2 | Vetor Resultante |
|---|---|---|---|
| Força | 10N para direita | 5N para esquerda | 5N para direita |
| Deslocamento | 20m para norte | 30m para sul | 10m para sul |
Se a magnitude de um vetor for maior que a do outro, o vetor resultante terá o sentido do vetor de maior magnitude.
Comparação entre as Somas, 4 Exemplos De Soma De Vetores No Mesmo Sentidos Opostas
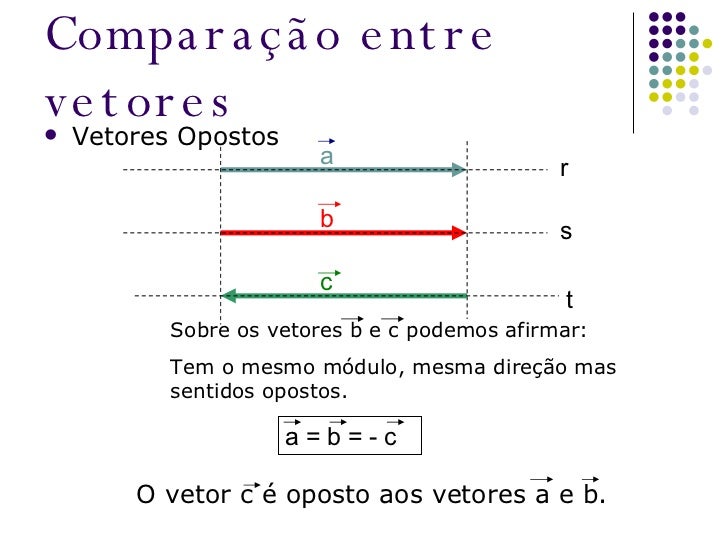
A principal diferença entre somar vetores com o mesmo sentido e sentidos opostos reside no cálculo da magnitude do vetor resultante. No primeiro caso, somamos as magnitudes; no segundo, subtraímos (considerando o maior menos o menor). A direção é a mesma em ambos os casos (na mesma linha de ação), mas o sentido pode variar dependendo dos sentidos dos vetores originais.
- Mesmo Sentido: Soma das magnitudes; sentido do vetor resultante é o mesmo dos vetores originais.
- Sentidos Opostos: Subtração das magnitudes (maior menos menor); sentido do vetor resultante é o do vetor de maior magnitude.
Exemplos Práticos
Vamos ver alguns exemplos práticos para consolidar nosso entendimento.
Exemplo 1 (Mesmo Sentido): Deslocamento Imagine uma pessoa caminhando 10 metros para leste, e depois mais 5 metros na mesma direção. O vetor resultante do deslocamento total será de 15 metros para leste. A representação gráfica seria duas setas apontando para leste, uma com 10 unidades de comprimento e outra com 5 unidades, e o vetor resultante seria uma seta com 15 unidades de comprimento, na mesma direção e sentido.
Exemplo 2 (Sentidos Opostos): Forças Considere um objeto sujeito a duas forças: uma de 20N puxando para a direita e outra de 10N puxando para a esquerda. O vetor resultante será uma força de 10N para a direita. Graficamente, teríamos duas setas, uma para a direita com 20 unidades de comprimento e outra para a esquerda com 10 unidades. O vetor resultante seria uma seta para a direita com 10 unidades de comprimento.

