Teorema de Pitágoras: Aplicações e Exemplos Resolvidos: Dois Exemplos Resolvidos Sobre A Aplicação Do Teorama De Pitagoas
Dois Exemplos Resolvidos Sobre A Aplicação Do Teorama De Pitagoas – O Teorema de Pitágoras é uma pedra fundamental da geometria, com aplicações práticas em diversas áreas, desde a construção civil até a navegação. Ele estabelece uma relação fundamental entre os lados de um triângulo retângulo, permitindo o cálculo de comprimentos desconhecidos com base em comprimentos conhecidos. Compreender esse teorema é essencial para dominar conceitos geométricos e resolver problemas em diversas situações do dia a dia.
Introdução ao Teorema de Pitágoras
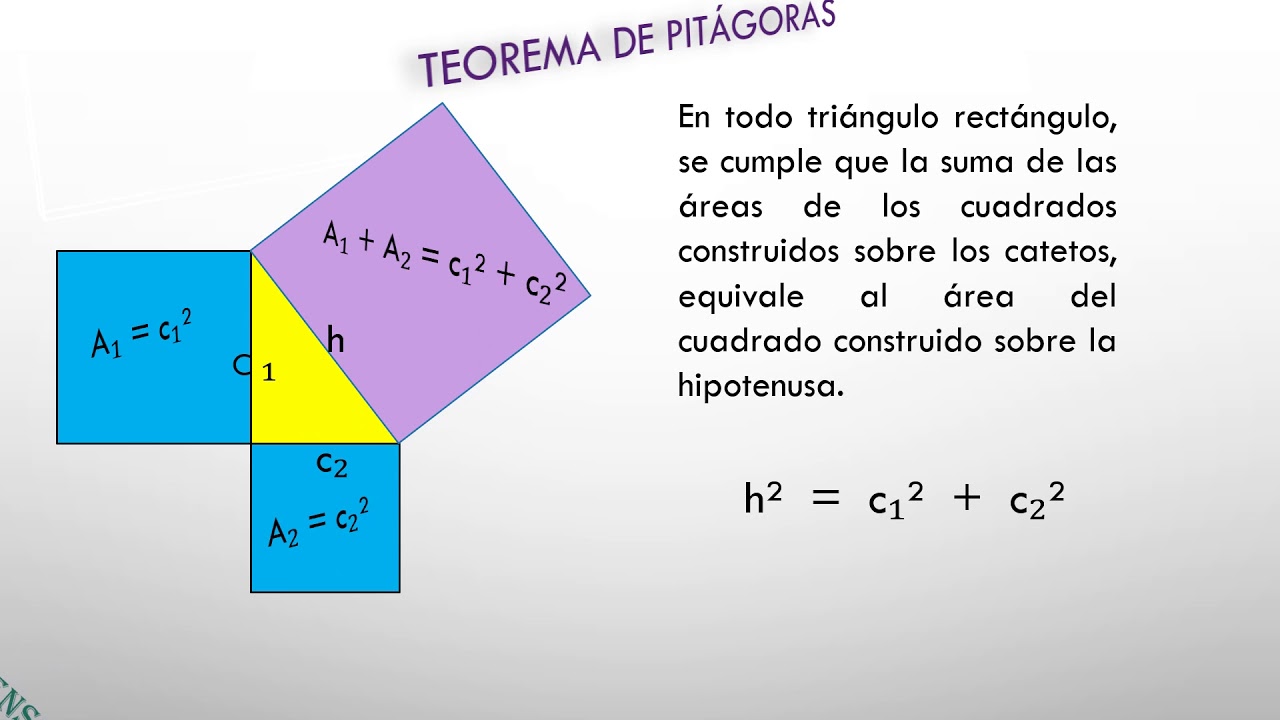
O Teorema de Pitágoras descreve a relação entre os três lados de um triângulo retângulo. Em um triângulo retângulo, os dois lados menores que formam o ângulo reto são chamados de catetos (geralmente representados por ‘a’ e ‘b’), e o lado maior oposto ao ângulo reto é chamado de hipotenusa (representada por ‘c’). O teorema afirma que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Essa relação é expressa pela famosa fórmula:
a² + b² = c²
Primeiro Exemplo Resolvido: Encontrando a Hipotenusa
Vamos calcular a hipotenusa de um triângulo retângulo com catetos de 3 cm e 4 cm. A aplicação direta da fórmula do Teorema de Pitágoras nos fornecerá a solução.
| Passo | Descrição | Cálculo | Resultado |
|---|---|---|---|
| 1 | Identificar os valores dos catetos | a = 3 cm, b = 4 cm | a = 3, b = 4 |
| 2 | Aplicar o Teorema de Pitágoras | c² = a² + b² | c² = 3² + 4² |
| 3 | Efetuar os cálculos | c² = 9 + 16 | c² = 25 |
| 4 | Calcular a raiz quadrada | c = √25 | c = 5 cm |
Segundo Exemplo Resolvido: Encontrando um Cateto, Dois Exemplos Resolvidos Sobre A Aplicação Do Teorama De Pitagoas
Agora, vamos determinar o comprimento de um cateto em um triângulo retângulo onde a hipotenusa mede 10 cm e um dos catetos mede 6 cm. Neste caso, precisaremos isolar a variável desconhecida na fórmula do Teorema de Pitágoras.
- Identificar os valores conhecidos: hipotenusa (c = 10 cm) e um cateto (a = 6 cm).
- Substituir os valores conhecidos na fórmula: 10² = 6² + b²
- Resolver a equação para b: 100 = 36 + b²
- Isolar b²: b² = 100 – 36 = 64
- Calcular a raiz quadrada: b = √64 = 8 cm
Aplicação em Problemas Práticos

O Teorema de Pitágoras é amplamente utilizado na construção civil. Imagine um construtor que precisa verificar se um pilar está perpendicular ao solo. Ele pode medir a distância horizontal (cateto a), a distância vertical (cateto b) e aplicar o Teorema de Pitágoras para calcular a hipotenusa (c), que representa a distância diagonal. Se a medida da hipotenusa calculada coincidir com a medida real da diagonal, o pilar estará perfeitamente perpendicular.
Problema: Um construtor precisa verificar se um pilar de 5 metros de altura está perpendicular ao solo. Ele mede 3 metros de distância horizontal da base do pilar. Usando o Teorema de Pitágoras, calcule a distância diagonal (hipotenusa) e determine se o pilar está perpendicular.
Solução: a = 3m, b = 5m. c² = 3² + 5² = 9 + 25 = 34. c = √34 ≈ 5,83 metros. Um método alternativo seria usar um esquadro de pedreiro. O Teorema de Pitágoras, entretanto, fornece um cálculo preciso e matematicamente fundamentado.
Ilustração Geométrica dos Exemplos
Primeiro Exemplo: Imagine um triângulo retângulo com catetos de 3 cm e 4 cm. Visualize um quadrado com lado 3 cm adjacente a um quadrado com lado 4 cm, formando um ângulo reto. A hipotenusa, de 5 cm, representa a diagonal que conecta os cantos opostos dos dois quadrados. A área do quadrado formado pela hipotenusa (25 cm²) é igual à soma das áreas dos quadrados formados pelos catetos (9 cm² + 16 cm² = 25 cm²).
Segundo Exemplo: Imagine um triângulo retângulo com hipotenusa de 10 cm e um cateto de 6 cm. Visualize um quadrado com lado 10 cm, representando a hipotenusa. Um quadrado com lado 6 cm representa o cateto conhecido. O cateto desconhecido, de 8 cm, representa o lado do quadrado restante que, junto com o quadrado de 6 cm, completa a área do quadrado maior (100 cm²).
Discussão sobre as Limitações do Teorema

O Teorema de Pitágoras aplica-se exclusivamente a triângulos retângulos. Em triângulos com outros tipos de ângulos, outras relações trigonométricas devem ser utilizadas. A compreensão precisa dos conceitos geométricos, como a identificação correta da hipotenusa e dos catetos, é crucial para a aplicação correta do teorema. A aplicação direta do Teorema de Pitágoras em problemas que envolvem geometria espacial mais complexa pode ser insuficiente, exigindo a utilização de outros métodos e conceitos geométricos.
Esperamos que, após a análise detalhada desses dois exemplos resolvidos, a aplicação do Teorema de Pitágoras tenha se tornado mais clara e acessível. Dominar este teorema é fundamental para o entendimento de diversos conceitos matemáticos e sua aplicação em diferentes áreas, desde a engenharia até a arquitetura. Lembre-se: a prática leva à perfeição! Resolva mais exercícios, explore diferentes problemas e, em breve, você estará aplicando o Teorema de Pitágoras com naturalidade e eficiência.
Boa sorte e até a próxima aventura matemática!

