Exemplo De Funções Exponenciais Sendo Utilizadas No Dia A Dia: Mais do que um conceito abstrato da matemática, as funções exponenciais permeiam nosso cotidiano, modelando fenômenos de crescimento e decaimento que impactam diretamente nossas vidas. Desde o crescimento populacional e a acumulação de juros compostos até a desintegração radioativa e a propagação de vírus, a presença dessas funções é constante, revelando padrões ocultos por trás de eventos aparentemente aleatórios.
Compreender seu funcionamento nos permite prever tendências, tomar decisões mais informadas e até mesmo modelar cenários futuros com maior precisão.
Neste artigo, exploraremos diversos exemplos práticos de como as funções exponenciais são aplicadas no dia a dia, desvendando sua utilidade em diferentes áreas, de finanças a epidemiologia. Veremos como modelos matemáticos simples, baseados em equações exponenciais, podem descrever com razoável precisão a evolução de diversos processos, desde o crescimento de um investimento até a diminuição da quantidade de um material radioativo ao longo do tempo.
Funções Exponenciais no Dia a Dia: Exemplo De Funções Exponenciais Sendo Utilizadas No Dia A Dia
As funções exponenciais, embora possam parecer complexas à primeira vista, estão presentes em diversas situações do nosso cotidiano, modelando fenômenos de crescimento e decaimento. Compreender seus princípios é fundamental para analisar e prever comportamentos em áreas como finanças, biologia e até mesmo na propagação de doenças. Neste artigo, exploraremos o conceito de funções exponenciais e analisaremos exemplos práticos de sua aplicação no dia a dia.
Introdução às Funções Exponenciais
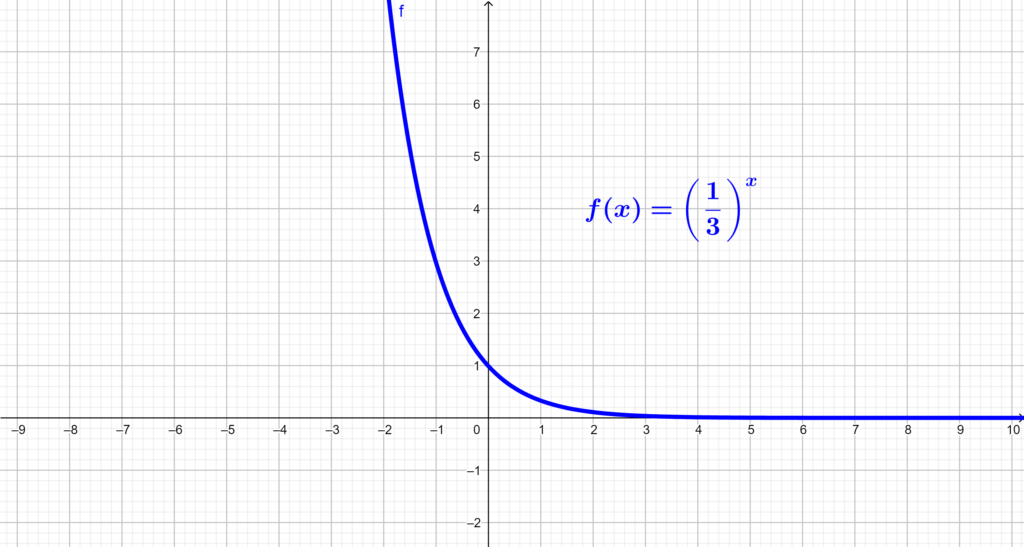
Uma função exponencial é uma função matemática onde a variável independente aparece no expoente. Sua forma geral é representada por f(x) = a, onde ‘a’ é a constante inicial, ‘b’ é a base (uma constante positiva e diferente de 1), e ‘x’ é o expoente (a variável independente). Se ‘b’ > 1, temos um crescimento exponencial; se 0 < 'b' < 1, temos um decaimento exponencial. Por exemplo,
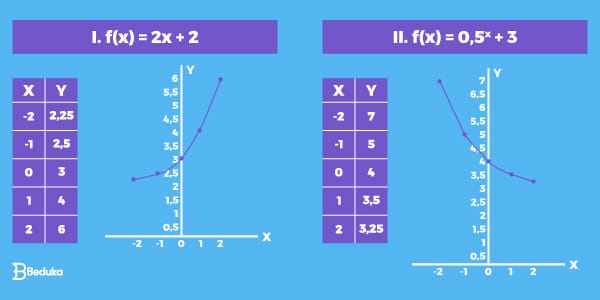
- b xf(x) = 2x representa um crescimento exponencial, enquanto f(x) = (1/2)x representa um decaimento exponencial.
O crescimento exponencial caracteriza-se por um aumento acelerado ao longo do tempo, enquanto o decaimento exponencial representa uma diminuição acelerada. Um exemplo de crescimento exponencial é a multiplicação de bactérias em uma cultura, enquanto um exemplo de decaimento exponencial é a desintegração radioativa de um elemento.
Exemplos no Dia a Dia: Crescimento Populacional
O crescimento populacional de uma cidade pode ser, em um primeiro momento, modelado por uma função exponencial. Imagine uma cidade com população inicial de 100.000 habitantes e uma taxa de crescimento anual de 2%. Podemos representar isso pela função: P(t) = 100000, onde P(t) é a população após t anos.
- (1.02) t
Comparando este modelo com dados reais, notaremos desvios. O modelo exponencial não considera fatores limitantes como recursos naturais, espaço físico ou políticas de controle de natalidade, que influenciam o crescimento populacional a longo prazo. Um modelo mais realista precisaria incorporar esses fatores.
| Ano | População (Modelo Exponencial) | População (Modelo Exponencial) | População (Modelo Exponencial) |
|---|---|---|---|
| 0 | 100000 | 100000 | 100000 |
| 1 | 102000 | 102000 | 102000 |
| 2 | 104040 | 104040 | 104040 |
| 3 | 106121 | 106121 | 106121 |
| 4 | 108243 | 108243 | 108243 |
| 5 | 110408 | 110408 | 110408 |
| 6 | 112616 | 112616 | 112616 |
| 7 | 114869 | 114869 | 114869 |
| 8 | 117166 | 117166 | 117166 |
| 9 | 119509 | 119509 | 119509 |
| 10 | 121800 | 121800 | 121800 |
Exemplos no Dia a Dia: Juros Compostos
Juros compostos são calculados sobre o valor principal mais os juros acumulados anteriormente. A fórmula para calcular o montante final (M) de um investimento com juros compostos é dada por: M = P (1 + i)n, onde P é o principal, i é a taxa de juros por período e n é o número de períodos.
Comparando com juros simples (onde os juros são calculados apenas sobre o principal), o crescimento de um investimento com juros compostos é exponencialmente maior a longo prazo. Um gráfico mostrando ambos os tipos de juros apresentaria uma linha reta para juros simples e uma curva ascendente, cada vez mais íngreme, para juros compostos.
Exemplo: Um investimento de R$10.000,00 a uma taxa de 10% ao ano, composto anualmente, após 5 anos resultaria em: M = 10000 (1 + 0.1)5 = 16105,10 . O cálculo é feito aplicando a taxa de juros cumulativamente a cada ano.
Exemplos no Dia a Dia: Desintegração Radioativa, Exemplo De Funções Exponenciais Sendo Utilizadas No Dia A Dia
A desintegração radioativa segue um decaimento exponencial, definido pela meia-vida, que é o tempo necessário para que metade da quantidade de um isótopo radioativo se desintegre. A fórmula geral para o decaimento radioativo é dada por: N(t) = N0, onde N(t) é a quantidade restante após o tempo t, N 0 é a quantidade inicial, e T é a meia-vida.
- (1/2) t/T
O Carbono-14, por exemplo, tem uma meia-vida de aproximadamente 5.730 anos. Sua taxa de decaimento pode ser modelada por uma função exponencial, permitindo a datação de artefatos arqueológicos.
- Após 1 meia-vida (5730 anos): 50% restante.
- Após 2 meias-vidas (11460 anos): 25% restante.
- Após 3 meias-vidas (17190 anos): 12,5% restante.
- Após 4 meias-vidas (22920 anos): 6,25% restante.
Exemplos no Dia a Dia: Propagação de Vírus e Epidemias (modelo simplificado)
Em um modelo simplificado, a propagação de um vírus pode ser aproximada por uma função exponencial, considerando uma taxa de contágio constante e uma população suscetível grande. No entanto, esse modelo é limitado, pois não considera fatores como imunidade, isolamento social ou a diminuição da população suscetível ao longo do tempo.
Exemplo hipotético: Se a taxa de contágio for de 2 pessoas por dia por cada infectado, e iniciarmos com 1 infectado, o número de infectados após t dias pode ser aproximado por I(t) = 2t. Este modelo, porém, rapidamente se torna irrealístico, pois o número de infectados cresce exponencialmente sem limites.
Exemplos no Dia a Dia: Valorização/Desvalorização de Bens
O valor de alguns bens, como carros e obras de arte, pode variar exponencialmente com o tempo. A valorização ou desvalorização depende de fatores como a demanda, a escassez, a inflação e a condição do bem. Uma função exponencial pode ser usada para modelar essa variação, considerando uma taxa de crescimento ou decaimento anual.
Por exemplo, um carro novo geralmente desvaloriza rapidamente nos primeiros anos, enquanto uma obra de arte de um artista renomado pode valorizar exponencialmente ao longo do tempo, dependendo da sua raridade e demanda no mercado de arte.

