Relações Métricas No Triângulo Retângulo Exemplos Resolvidos, este estudo aprofunda as relações entre os lados e a altura de um triângulo retângulo, explorando conceitos como o Teorema de Pitágoras e relações métricas fundamentais. O objetivo é fornecer uma compreensão profunda e prática dessas relações, através de exemplos resolvidos que ilustram a aplicação em problemas geométricos e situações reais.
O estudo das relações métricas no triângulo retângulo é essencial para a compreensão de diversos conceitos geométricos e para a resolução de problemas que envolvem figuras geométricas. Através da aplicação do Teorema de Pitágoras e das relações métricas fundamentais, é possível determinar o comprimento de lados, a altura e outras medidas importantes de um triângulo retângulo.
Introdução às Relações Métricas no Triângulo Retângulo
O estudo das relações métricas no triângulo retângulo é fundamental para a resolução de problemas geométricos que envolvem esse tipo de triângulo. As relações métricas estabelecem conexões entre os lados e a altura do triângulo retângulo, permitindo calcular medidas desconhecidas a partir de outras já conhecidas.
Terminologia Fundamental, Relações Métricas No Triângulo Retângulo Exemplos Resolvidos
O triângulo retângulo é um triângulo que possui um ângulo reto (90°). Os lados que formam o ângulo reto são chamados de catetos, e o lado oposto ao ângulo reto é a hipotenusa. A altura relativa à hipotenusa é o segmento de reta perpendicular à hipotenusa que passa pelo vértice do ângulo reto.
As projeções dos catetos sobre a hipotenusa são os segmentos de reta que se formam sobre a hipotenusa quando traçamos a altura relativa à hipotenusa.
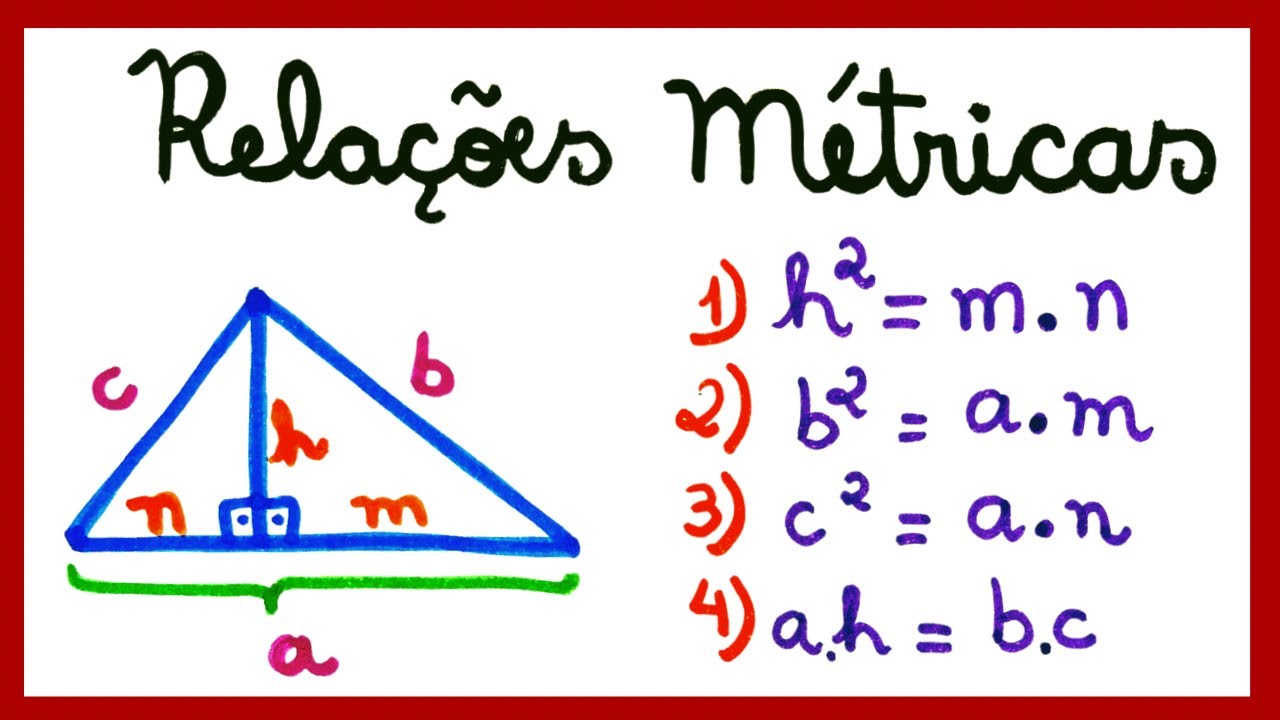
Os catetos são representados por a e b, a hipotenusa por c, a altura relativa à hipotenusa por h, e as projeções dos catetos sobre a hipotenusa por m e n.
Importância das Relações Métricas
As relações métricas no triângulo retângulo são ferramentas importantes para a resolução de problemas geométricos, pois permitem:
- Calcular o comprimento de lados e altura desconhecidos;
- Determinar a área do triângulo retângulo;
- Encontrar as medidas dos ângulos do triângulo;
- Resolver problemas de geometria plana e espacial.
Teorema de Pitágoras e suas Aplicações
O Teorema de Pitágoras é um dos teoremas mais importantes da geometria e tem aplicações em diversas áreas, desde a construção civil até a navegação espacial. Ele estabelece uma relação fundamental entre os lados de um triângulo retângulo, sendo crucial para o cálculo de distâncias, áreas e volumes.
Demonstração do Teorema de Pitágoras
O Teorema de Pitágoras afirma que, em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos (os lados adjacentes ao ângulo reto).
Em um triângulo retângulo, com hipotenusa ce catetos ae b, temos: c² = a² + b².
A demonstração do Teorema de Pitágoras pode ser feita através de diversas abordagens, como a construção de quadrados sobre os lados do triângulo retângulo e a comparação de suas áreas.
Aplicações do Teorema de Pitágoras
O Teorema de Pitágoras pode ser aplicado em diversos problemas práticos, como:
- Determinar o comprimento da diagonal de um retângulo:
- Calcular a distância entre dois pontos no plano cartesiano:
- Encontrar a altura de um triângulo equilátero:
- Calcular o comprimento de uma escada apoiada em uma parede:
Exemplos Resolvidos
Exemplo 1: Determinando o comprimento da hipotenusa
Um triângulo retângulo possui catetos com medidas de 3 cm e 4 cm. Qual o comprimento da hipotenusa? Solução:Utilizando o Teorema de Pitágoras: c² = a² + b²c² = 3² + 4²c² = 9 + 16c² = 25c = √25c = 5 cmPortanto, o comprimento da hipotenusa é 5 cm.
Exemplo 2: Calcular a distância entre dois pontos no plano cartesiano
Determine a distância entre os pontos A (2, 1) e B (5, 4). Solução:A distância entre dois pontos no plano cartesiano pode ser calculada utilizando o Teorema de Pitágoras. Imagine um triângulo retângulo formado pelos pontos A, B e C, onde C tem coordenadas (5, 1).O cateto AC tem comprimento 3 (diferença entre as abscissas de A e C) e o cateto BC tem comprimento 3 (diferença entre as ordenadas de B e C).
Aplicando o Teorema de Pitágoras: AB² = AC² + BC²AB² = 3² + 3²AB² = 9 + 9AB² = 18AB = √18AB = 3√2Portanto, a distância entre os pontos A e B é 3√2.
Exemplo Prático
Imagine que você está construindo uma casa e precisa instalar uma escada que irá do chão até o telhado. A altura da parede é de 3 metros e você deseja que a escada fique a 1 metro de distância da parede.
Qual o comprimento mínimo da escada? Solução:Utilizando o Teorema de Pitágoras, podemos calcular o comprimento da escada (hipotenusa): c² = a² + b²c² = 3² + 1²c² = 9 + 1c² = 10c = √10c ≈ 3,16 metrosPortanto, o comprimento mínimo da escada é de aproximadamente 3,16 metros.
Relações Métricas Fundamentais: Relações Métricas No Triângulo Retângulo Exemplos Resolvidos

As relações métricas no triângulo retângulo são fórmulas que relacionam os lados e as alturas do triângulo. Essas relações são essenciais para a resolução de problemas que envolvem triângulos retângulos, sendo ferramentas importantes na geometria plana.
Relações Métricas Fundamentais
As relações métricas fundamentais são derivadas do Teorema de Pitágoras e permitem calcular as medidas de lados, alturas e projeções no triângulo retângulo.
| Relação | Descrição | Fórmula | Ilustração |
|---|---|---|---|
| Altura relativa à hipotenusa | A altura relativa à hipotenusa de um triângulo retângulo divide a hipotenusa em dois segmentos, e o quadrado da altura é igual ao produto desses segmentos. | h² = m.n | Imagine um triângulo retângulo ABC, com ângulo reto em C. A altura relativa à hipotenusa, h, divide a hipotenusa AB em dois segmentos, m e n. A relação métrica afirma que h² é igual ao produto de m e n. |
| Cateto relativo à hipotenusa | O quadrado de um cateto é igual ao produto da hipotenusa pelo segmento da hipotenusa adjacente ao cateto. | a² = c.m, b² = c.n | No mesmo triângulo retângulo ABC, a² é igual ao produto da hipotenusa c pelo segmento m, e b² é igual ao produto da hipotenusa c pelo segmento n. |
Demonstração:Para demonstrar a relação h² = m.n, podemos usar o Teorema de Pitágoras em dois triângulos retângulos menores formados pela altura:
Triângulo ACH
h² + m² = a²
Triângulo BCH
h² + n² = b²Somando as duas equações, obtemos: 2h² + m² + n² = a² + b².Aplicando o Teorema de Pitágoras no triângulo ABC, temos: a² + b² = c².Substituindo na equação anterior, temos: 2h² + m² + n² = c².Como c = m + n, temos: 2h² + m² + n² = (m + n)².Expandindo o lado direito da equação, temos: 2h² + m² + n² = m² + 2mn + n².Simplificando, obtemos: 2h² = 2mn.Portanto, h² = m.n.As outras relações métricas podem ser demonstradas de forma similar.
Exemplos de Aplicações
As relações métricas podem ser usadas para resolver uma variedade de problemas envolvendo triângulos retângulos, como calcular a altura de um triângulo, a medida de um lado, ou a área de um triângulo. Exemplo 1:Um triângulo retângulo tem hipotenusa de 10 cm e um cateto de 6 cm.
Calcule a altura relativa à hipotenusa. Solução:Usando a relação h² = m.n, temos: h² = 6.4 = 24.Portanto, h = √24 = 2√6 cm. Exemplo 2:Um triângulo retângulo tem hipotenusa de 12 cm e um dos segmentos da hipotenusa é 3 cm.
Calcule o cateto adjacente a esse segmento. Solução:Usando a relação a² = c.m, temos: a² = 12.3 = 36.Portanto, a = √36 = 6 cm.
Relações Métricas e Semelhança de Triângulos
A semelhança de triângulos é uma ferramenta fundamental para a compreensão e dedução das relações métricas no triângulo retângulo. A relação entre esses dois conceitos reside no fato de que triângulos semelhantes possuem ângulos correspondentes congruentes e lados proporcionais, o que permite estabelecer relações entre os seus elementos.
Dedução das Relações Métricas a partir da Semelhança de Triângulos
A semelhança de triângulos pode ser utilizada para deduzir as relações métricas no triângulo retângulo. Para isso, podemos considerar os seguintes triângulos semelhantes:
- O triângulo retângulo original (ABC), onde AB é a hipotenusa, AC é um cateto e BC é o outro cateto.
- O triângulo retângulo formado pela altura relativa à hipotenusa (AH) e o cateto AC (ACH), onde AH é a altura, AC é a base e CH é a projeção do cateto AC sobre a hipotenusa.
- O triângulo retângulo formado pela altura relativa à hipotenusa (AH) e o cateto BC (ABH), onde AH é a altura, BC é a base e BH é a projeção do cateto BC sobre a hipotenusa.
A semelhança entre esses triângulos permite estabelecer as seguintes relações:
AC/AB = AH/AC
BC/AB = AH/BC
AC/CH = AB/AC
BC/BH = AB/BC
Essas relações podem ser reescritas para obter as relações métricas fundamentais:
AC² = AB
CH
BC² = AB
BH
AH² = CH
BH
Exemplo de Aplicação da Semelhança de Triângulos
Considere um triângulo retângulo ABC, onde AB é a hipotenusa, AC é um cateto de comprimento 6 cm e BC é o outro cateto de comprimento 8 cm. A altura relativa à hipotenusa é AH.Utilizando a semelhança entre os triângulos ABC, ACH e ABH, podemos calcular o comprimento da altura AH e as projeções CH e BH.Primeiro, podemos usar a relação AC²/AB = AH/AC para calcular AH:
AH = AC²/AB = 6²/10 = 3,6 cm
Em seguida, podemos usar as relações AC/CH = AB/AC e BC/BH = AB/BC para calcular CH e BH:
CH = AC²/AB = 6²/10 = 3,6 cm
BH = BC²/AB = 8²/10 = 6,4 cm
Portanto, a altura relativa à hipotenusa é 3,6 cm, a projeção do cateto AC sobre a hipotenusa é 3,6 cm e a projeção do cateto BC sobre a hipotenusa é 6,4 cm.
Query Resolution
Quais são as principais relações métricas no triângulo retângulo?
As principais relações métricas são: o Teorema de Pitágoras, a relação entre a altura e os catetos, a relação entre a altura e a hipotenusa, e as relações entre os segmentos formados pela altura na hipotenusa.
Como posso aplicar as relações métricas na resolução de problemas?
As relações métricas podem ser aplicadas para determinar o comprimento de lados, a altura e outras medidas importantes de um triângulo retângulo. Para resolver um problema, é necessário identificar as relações métricas relevantes e aplicá-las de acordo com as informações fornecidas.
Quais são os benefícios de estudar as relações métricas no triângulo retângulo?
O estudo das relações métricas no triângulo retângulo proporciona uma compreensão profunda de conceitos geométricos, além de desenvolver habilidades de resolução de problemas que podem ser aplicadas em diversas áreas do conhecimento.

